Distribusi frekuensi adalah metode penting dalam statistika untuk menyusun dan meringkas data agar lebih mudah dianalisis. Di artikel ini, Anda akan mempelajari definisi distribusi frekuensi, jenis-jenisnya, cara membuat tabel distribusi frekuensi, serta contoh soal lengkap dengan jawaban yang membantu memperdalam pemahaman.
Dengan memahami topik ini, Anda dapat mengelola data dengan lebih efektif dan mendapatkan insight yang jelas dari hasil penelitian.
Apa Itu Distribusi Frekuensi?
Distribusi frekuensi adalah cara sederhana untuk menyusun, meringkas, dan mengatur data hasil penelitian agar lebih mudah dipahami oleh peneliti. Kata “distribusi” berasal dari bahasa Inggris “distribution” yang berarti pembagian atau penyaluran, sedangkan “frekuensi” dalam statistika merujuk pada jumlah kemunculan suatu nilai dalam data.
Prinsip dasar distribusi frekuensi adalah bagaimana nilai-nilai angka dari variabel tersebut dapat tersalurkan, tersebar, terbagi, dan terpancar dalam sebuah tabel atau grafik.
Jenis-jenis Distribusi Frekuensi
Terdapat beberapa jenis distribusi frekuensi yaitu:
1. Distribusi Frekuensi Biasa
Didapat dari setiap kelompok data dan berisikan jumlah frekuensi
2. Distribusi Frekuensi Relatif
Distribusi frekuensi relatif berisikan nilai-nilai dari hasil bagi frekuensi kelas dan juga jumlah pengamatan, selain itu juga proporsi data pada suatu kelas interval dapat dinyatakan dengan tabel ini. Cara yang digunakan adalah dengan membagi frekuensi dengan total data pengamatan atau observasi.
3. Distribusi Frekuensi Kumulatif
Isi dari frekuensi kumulatif yaitu frekuensi yang telah dijumlahkan. Kurva yang terdapat pada distribusi ini disebut dengan kurva ogif. Distribusi frekuensi ini mempunyai dua macam yaitu frekuensi kurang dari (<) dan frekuensi lebih dari (>). Berikut contohnya:
Dari contoh tabel distribusi frekuensi di bawah ini, buatlah tabel distribusi frekuensi kumulatif kurang dari (<) dan lebih dari (>).
| Nilai | Frekuensi |
| 51-60 | 4 |
| 61-70 | 13 |
| 71-80 | 21 |
| 81-90 | 11 |
| 91-100 | 7 |
Jawab:
- Tabel distribusi frekuensi kumulatif kurang dari (<)
| Nilai | F. Kumulatif (<) |
| < 60,5 | 4 |
| < 70,5 | 4+13=17 |
| < 80,5 | 17+21=38 |
| < 90,5 | 38+11=49 |
| < 100,5 | 49+7=56 |
60,5 sampai 100,5 didapat dari rumus tepi atas, yaitu:
Ta=b+0,5
60+0,5
60,5
Ta=b+0,5
70+0,5
70,5
Sampai seterusnya!
- Tabel distribusi frekuensi kumulatif lebih dari (>)
| Nilai | F. Kumulatif (<) |
| < 50,5 | 56 |
| < 60,5 | 56-4=52 |
| < 70,5 | 52-13=39 |
| < 80,5 | 39-21=18 |
| < 90,5 | 18-11=7 |
50,5-90,5 didapat dari rumus tepi bawah, yaitu:
Tb=a-0,5
51-0,5
50,5
Tb=a-0,5
61-0,5
60,5
Sampai seterusnya!
Untuk data berukuran besar, gunakan tabel frekuensi kelompok. Sedangkan untuk data kecil, pakai tabel frekuensi tidak dikelompokkan.
Beberapa langkah penting membuat tabel distribusi frekuensi kelompok:
1. Menentukan jangkauan data (j)
j = Xmax – Xmin (selisih antara nilai maksimum dan minimum).
2. Menentukan banyak kelas interval (k)
Gunakan rumus:
k = 1 + 3,3 log n (n = jumlah data).
3. Menentukan panjang kelas interval (p)
p = j / k
Sesuaikan dengan tingkat ketelitian data (satuan/desimal).
4. Menentukan batas kelas interval
Batas bawah kelas pertama = datum terkecil.
Batas atas kelas = kelipatan panjang kelas.
5. Menentukan batas bawah nyata dan batas atas nyata
- Jika data satuan: tepi bawah = batas bawah – 0,5; tepi atas = batas atas + 0,5.
- Jika data satu desimal: tepi bawah = batas bawah – 0,05; tepi atas = batas atas + 0,05.
- Jika data dua desimal: tepi bawah = batas bawah – 0,005; tepi atas = batas atas + 0,005.
6. Menentukan frekuensi dan titik tengah interval
Titik tengah = ½ (batas bawah + batas atas).
Untuk tabel frekuensi tidak dikelompokkan:
- Buat tabel dua kolom dengan label variabel dan frekuensi.
- Hitung frekuensi masing-masing nilai dan isi di kolom frekuensi.
Visualisasi Distribusi Frekuensi dengan Histogram
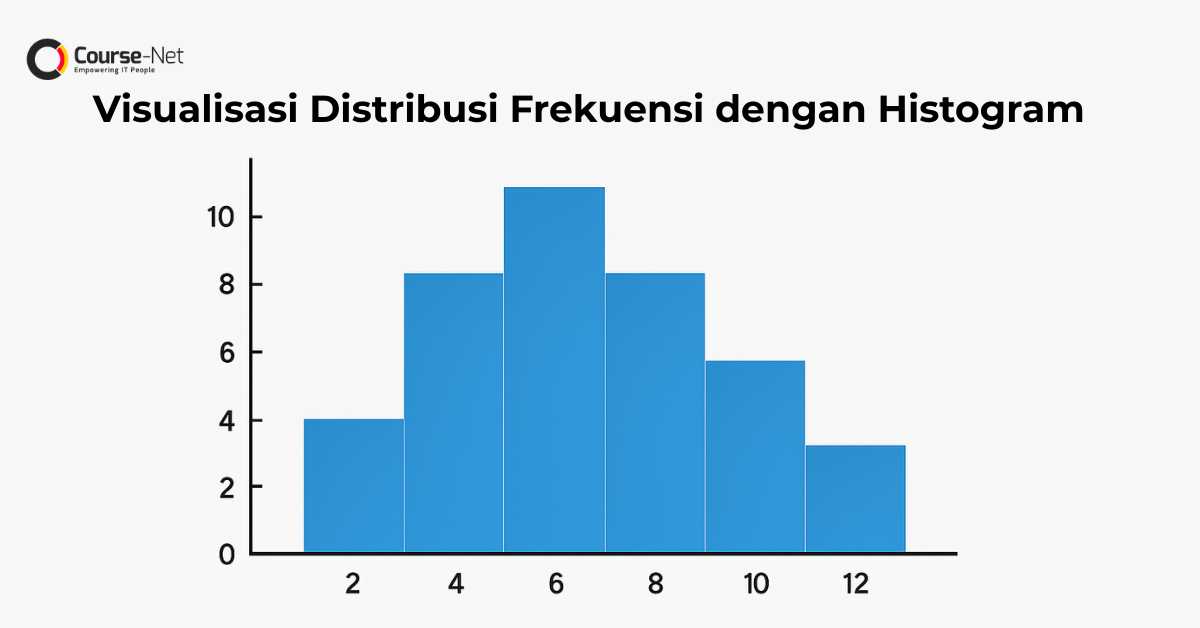
Histogram adalah grafik yang umum digunakan untuk memvisualisasikan distribusi frekuensi data. Dengan menggunakan batang-batang yang mewakili frekuensi pada setiap interval kelas, histogram membantu pembaca melihat pola sebaran data secara visual, seperti konsentrasi data, variasi, dan potensi outlier. Histogram memudahkan interpretasi data dibandingkan hanya melihat tabel angka.
Contoh Soal Distribusi Frekuensi dan Jawabannya
Data merupakan elemen pokok yang ada pada analisis statistik. Metode yang digunakan dalam mengelola data agar memudahkan analisis yaitu menggunakan distribusi frekuensi dengan menggolongkan data mentah dan penggambarannya menggunakan grafik.
Alat yang digunakan untuk mengatur dan merangkum data tentang sebaran nilai agar lebih jelas dan terperinci yaitu dengan menggunakan tabel distribusi frekuensi. Berikut merupakan contoh soal distribusi frekuensi dan jawabannya:
Contoh Soal Pilihan Ganda
Perhatikan tabel distribusi frekuensi variabel acak x berikut!
| Nilai | Frekuensi |
| 21-30 | 2 |
| 31-40 | 8 |
| 41-50 | 9 |
| 52-60 | 6 |
| 61-70 | 3 |
| 71-80 | 2 |
| 81-90 | 8 |
| 91-10 | 6 |
Dari data di atas mencerminkan hasil ujian Bahasa Indonesia yang dilakukan oleh 44 siswa dari kelas XII IPS SMAN 10 Jakarta Selatan. Dengan batas kelulusan yang ditetapkan pada 71, maka berapa banyak siswa yang berhasil lulus?
- 25
- 14
- 10
- 16
- 19
Contoh Soal Uraian
Diberikan data mengenai nilai ulangan harian Matematika 20 siswa di sebuah kelas sebagai berikut: 78, 85, 89, 72, 75, 88, 80, 90, 84, 77, 86, 74, 91, 82, 79, 88, 76, 90, 83, 85. Buatlah tabel distribusi frekuensi untuk kategori nilai sebagai berikut:
70-74
75-79
80-84
85-89
90-94
Setelah itu, jawablah pertanyaan berikut:
- Berapakah frekuensi siswa yang mendapatkan nilai antara 80-84?
- Kategori nilai manakah yang memiliki frekuensi terbanyak?
- Berapakah jumlah siswa yang mendapatkan nilai 85 ke atas?
Jawaban:
Berikut tabel distribusi frekuensi dari data sesuai dengan kategori yang diberikan:
| Kategori Nilai | Frekuensi (f) |
| 70-74 | 2 |
| 75-79 | 4 |
| 80-84 | 5 |
| 85-89 | 5 |
| 90-94 | 4 |
| Total | 20 |
- Besar frekuensi siswa yang mendapatkan nilai antara 80-84 adalah 5 siswa
- Kategori nilai yang memiliki frekuensi terbanyak adalah kategori nilai 80-84 dan 85-89 keduanya memiliki frekuensi terbanyak yaitu 5 siswa
- Jumlah siswa yang mendapatkan nilai 85 ke atas antara lain: 5 siswa (kategori 85-89) = 4 siswa (kategori 90-94) = 9 siswa.
Pelajari Lebih Dalam di Kelas Big Data Course-Net
Jika kamu tertarik memahami lebih jauh konsep statistik seperti distribusi frekuensi dan bagaimana data diolah secara profesional, kelas Big Data dari Course-Net adalah pilihan yang tepat. Di sana, kamu akan belajar langsung bagaimana analisis data dilakukan dalam skala besar, dengan pendekatan yang aplikatif dan dibimbing mentor berpengalaman.




