Regresi Linier dalam Analisis Big Data: Pengertian, Metode, Penerapan, dan Keunggulannya
Dari banyaknya informasi kompleks atau big data yang ada, masing-masing dari mereka menyimpan informasi berharga yang harus diketahui. Inilah mengapa analisis regresi linier dihadirkan sebagai salah satu alat analisis big data.
Adanya regresi linier juga memungkinkan Anda untuk dapat memahami hubungan antara dua variabel yang berbeda, memprediksi tren, dan membuat keputusan yang lebih baik berdasarkan data. Artikel ini akan menjelaskan secara mendalam tentang regresi linier, mulai dari pengertiannya, metode yang digunakan, penerapannya dalam analisis big data, hingga keunggulannya.
Baca Juga: Analisis Regresi Linier Sederhana: Strategi Efektif untuk Big Data
Apa itu Regresi Linier?
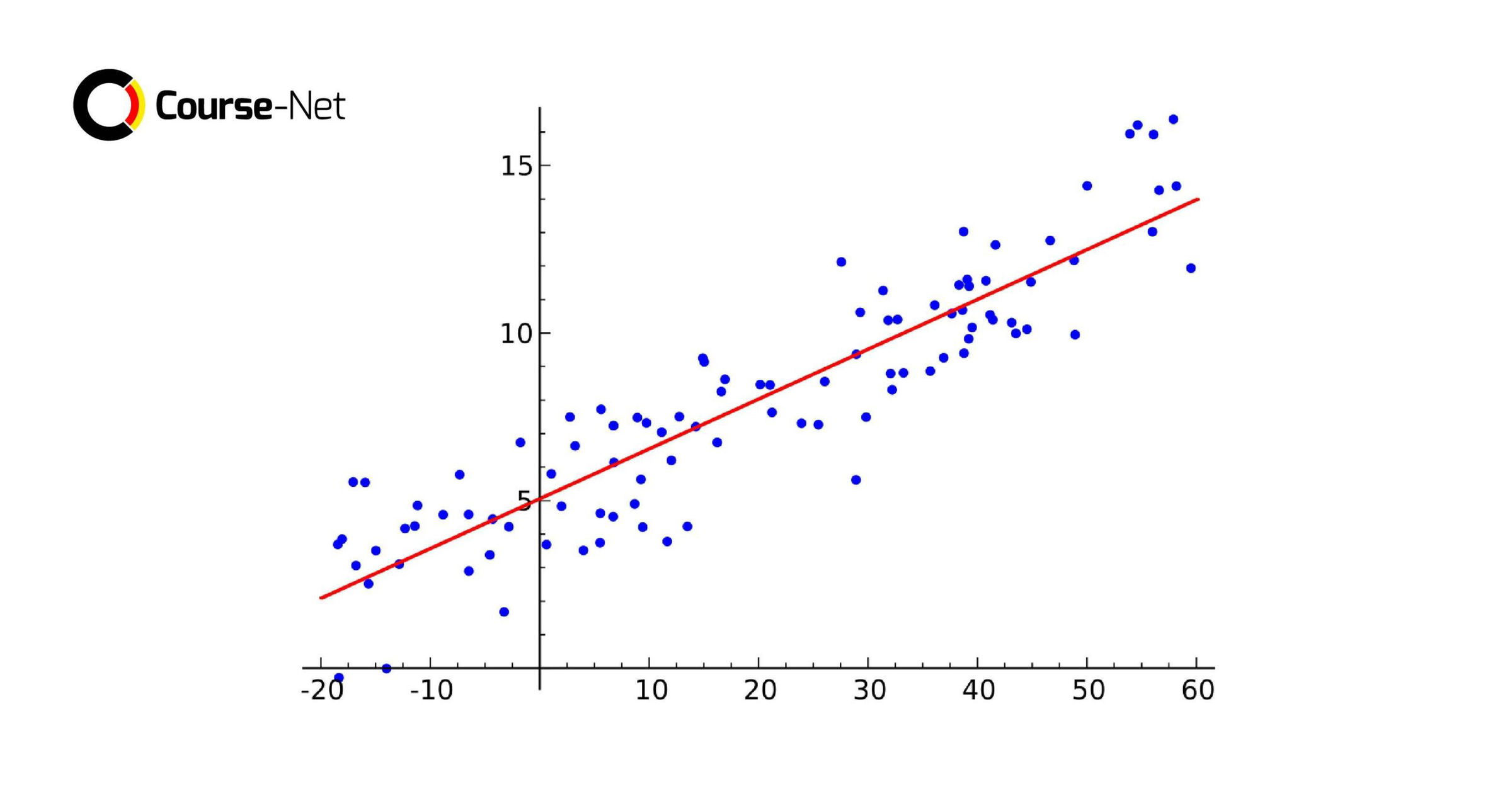
Regresi linier adalah teknik analisis statistik yang digunakan untuk memodelkan hubungan antara variabel dependen dan independen. Teknik analisis ini dapat mengasumsikan hubungan linier antara variabel-variabel tersebut dan mempresentasikannya dalam bentuk persamaan garis lurus atau yang disebut sebagai garis regresi.
5 Metode Regresi Linier
Saat menganalisis big data dengan teknik regresi linier, ada beberapa langkah-langkah yang perlu Anda ikuti. Berikut inilah langkah-langkah yang dimaksud:
Pengumpulan Data
Langkah pertama adalah mengumpulkan data yang relevan dengan variabel independen dan dependen yang ingin dianalisis. Data ini haruslah akurat dan representatif agar hasil analisis Anda dapat diandalkan.
Pemilihan Model
Setelah data berhasil terkumpul, langkah selanjutnya adalah memilih model regresi linear yang sesuai. Regresi linier dapat dibedakan menjadi dua kategori utama, yaitu regresi linier sederhana dan regresi linier berganda.
Estimasi Parameter
Dalam langkah ini, Anda akan menggunakan metode matematika, seperti metode kuadrat terkecil untuk mengestimasi nilai parameter dalam persamaan regresi linier. Parameter ini akan membantu mencerminkan hubungan antar variabel tersebut.
Evaluasi Model
Setelah model diestimasi, perlu dilakukan evaluasi untuk memastikan keakuratan dan ketepatannya. Beberapa metrik yang umum digunakan adalah R-squared, mean squared error (MSE), dan mean absolute error (MAE).
Interpretasi Hasil
Langkah terakhir adalah menginterpretasikan hasil analisis regresi linier. Dalam tahapan ini, Anda akan melibatkan makna koefisien regresi, signifikansi statistik, dan implikasi praktis dari hasil analisis.
Jenis-Jenis Regresi Linier
Terdapat dua jenis model regresi linier yang perlu Anda ketahui. Model ini dinamakan regresi linier sederhana dan berganda. Berikut inilah perbedaan antar kedua jenis regresi tersebut:
1. Regresi Linier Sederhana
Regresi linier sederhana digunakan ketika hanya ada satu variabel independen yang ingin dianalisis hubungannya dengan variabel dependen. Misalnya, ketika Anda ingin mengetahui hubungan antara jumlah jam belajar (variabel independen) dengan nilai ujian (variabel dependen).
2. Regresi Linier Berganda
Kemudian, jika Anda ingin menganalisis pengaruh beberapa variabel independen terhadap variabel dependen, maka regresi linier berganda adalah metode yang tepat. Contohnya adalah saat Anda ingin mengetahui hubungan antara pendapatan, tingkat pendidikan, dan pengalaman kerja (variabel independen) dengan tingkat kepuasan kerja (variabel dependen).
Rumus Regresi Linier
Rumus regresi linier merupakan cara untuk mengungkap hubungan antara dua variabel dalam analisis statistik. Dengan persamaan matematis sederhana, Anda dapat memprediksi nilai suatu variabel berdasarkan variabel lainnya.
Rumus Dasar
Rumus dasar regresi linier sederhana adalah sebagai berikut:
Y = β0 + β1X + ε
Di mana:
- Y merupakan variabel dependen
- X adalah variabel independen
- β0 merupakan intercept, nilai Y ketika X = 0
- β1 adalah koefisien regresi yang menunjukkan seberapa besar perubahan Y ketika X berubah satu satuan
- ε merepresentasikan error, yaitu selisih antara nilai prediksi dan nilai sebenarnya
Contoh Penggunaan Rumus
Sebagai contoh regresi, kita gunakan data tentang jumlah jam belajar (X) dan nilai ujian (Y) dari beberapa siswa:
- Jam Belajar berupa nilai X yang tercatat adalah 2, 3, 4, dan 5.
- Nilai Ujian Y yang tercatat adalah 70, 80, 90, dan 95.
Estimasi nilai β0 dan β1 dapat dilakukan dengan menggunakan metode kuadrat terkecil. Misalnya, kita mendapatkan β0 = 60 dan β1 = 7.5. Dengan demikian, persamaan regresi liniernya adalah: Y = 60 + 7.5X
Persamaan regresi yang dihasilkan ini dapat digunakan untuk memperkirakan nilai ujian siswa berdasarkan lamanya waktu belajar mereka. Sebagai contohnya, ketika seorang siswa belajar selama 6 jam, maka nilai ujian yang diprediksi adalah: Y = 60 + 7.5 * 6 = 105
Penerapan Regresi Linier dalam Big Data
Penerapan metode regresi memiliki beberapa peran dalam menganalisis big data, salah satunya adalah mengungkap informasi dalam data yang kompleks. Berikut inilah peran-perannya yang dimaksud:
Peran Regresi Linier dalam Big Data
Regresi linier berperan penting dalam analisis big data karena kemampuannya untuk mengungkap pola dan hubungan tersembunyi. Dalam konteks big data, regresi linier dapat digunakan untuk hal-hal berikut ini:
- Prediksi: Metode ini dapat memprediksi nilai variabel dependen berdasarkan variabel independen yang diketahui.
- Segmentasi: Kedua, metode ini dapat mengelompokkan data berdasarkan karakteristik tertentu yang relevan.
- Analisis Penyebab-Akibat: Memahami faktor-faktor yang mempengaruhi suatu variabel tertentu.
- Optimasi: Terakhir, metode ini akan membantu Anda menemukan nilai optimal dari nilai variabel independen untuk mencapai tujuan tertentu.
Tools dan Software untuk Melakukan Regresi Linier
Terdapat berbagai tools dan software yang dapat digunakan untuk melakukan analisis regresi linier pada big data, antara lain sebagai berikut:
- Python: Bahasa pemrograman populer ini memiliki library khusus seperti Scikit-learn dan Statsmodels untuk melakukan analisis regresi linier.
- R: Bahasa pemrograman ini dirancang khusus untuk analisis statistik, termasuk regresi linier.
- Apache Spark: Ketiga adalah framework big data yang menyediakan library MLlib untuk analisis regresi linier terdistribusi.
Keunggulan Regresi Linier
Apa saja keunggulan yang dimiliki oleh regresi linier? Regresi linier memiliki beberapa keunggulan, antara lain sebagai berikut:
- Sederhana dan Mudah Dipahami: Konsep regresi linier relatif mudah dipahami dan diinterpretasikan sehingga dapat digunakan oleh berbagai kalangan, baik dari latar belakang teknis maupun non-teknis.
- Efisien dalam Komputasi: Kedua, metode regresi linier ini dapat diimplementasikan secara efisien, bahkan pada data yang sangat besar.
- Beragam Aplikasi: Regresi linier dapat diaplikasikan dalam berbagai bidang, mulai dari bisnis, keuangan, hingga ilmu sosial.
Baca Juga: 10 Fungsi Metode Linear Regresssion Pada Machine Learning
Kesimpulan
Sebagai kesimpulannya, regresi linier merupakan sebuah alat yang sangat berharga untuk menganalisis big data. Dengan kemampuannya untuk mengungkap hubungan antara variabel-variabel dan memprediksi tren, metode ini sangat membantu Anda untuk mengambil keputusan berbasis data.
Untuk mengembangkan keahlian di bidang analisis big data, daftarkan diri Anda ke dalam Kursus Data Science dan Kursus Data Analyst di Course-Net sebagai pihak penyelenggara kursus IT terbaik di Indonesia.
Course-Net telah terbukti mendapatkan 4 kali penghargaan tingkat internasional, Dengan sistem pembelajaran experience practice based yang langsung diajarkan oleh coach praktisi kami yang sudah pasti memiliki pengalaman lebih dari 5 tahun di bidang IT. Anda juga akan mendapatkan benefit untuk bisa Re-Coaching belajar sampai bisa dengan cukup sekali bayar dan bisa dicicil maksimal 18 kali cicilan.
Sebanyak 100.000+ IT People dan 472+ corporate clients sudah membuktikan kepercayaan mereka dengan bergabung bersama kami. Apalagi, Course-Net juga sudah mendapatkan rating bintang 4.9 dari 15.000+ reviews di Google Review. Tunggu apalagi? Daftarkan dirimu di Kursus Data Science dan Kursus Data Analyst sekarang!